Введение

Термин "фрактал" происходит от латинского слова "fractio" — "разделяю на части". Этот термин был введен в современный научный лексикон Бенуа Б. Мандельбротом, сотрудником Исследовательского центра имени Томаса Дж. Уотсона корпорации IBM в Йорктаун-Хейтсе (шт. Нью-Йорк, США) в 1983 году в его книге «Фрактальная геометрия природы».

Фракталы дают чрезвычайно компактный способ описания объектов и процессов. Большинство структур, которые мы можем вычленить из реальных объектов, обладают свойством геометрической регулярности или самоподобием, что проявляется в их инвариантности по отношению к масштабу. Другими словами, если мы рассматриваем реальные объекты в разном масштабе, то на каждом уровне находим одни и те же геометрические формы.

Фрактальность реального мира проявляется не только в геометрическом смысле. Мы обнаруживаем подобие и на значительно более абстрактном философском уровне. Например, подобие структур на различных уровнях физической картины мира: от систем галактик и планетарных систем до планетарной модели атома Бора. Другим примером может служить универсальность математического описания реального мира, когда эквивалентные в математическом смысле уравнения оказываются пригодны для описания явлений и в электродинамике, и в механике, и в гидродинамике.

Следует, с другой стороны, акцентировать внимание на том, что в реальном мире никаких фракталов не существует, как не существует в реальном мире и актуальных бесконечностей, введенных в математику Георгом Кантором. Мы рассматриваем фракталы лишь в аспекте математической модели, пригодной для более-менее удобного описания реального мира.

Однако в данной работе мы остановимся на наиболее простых аспектах применения фракталов:

анализ регулярных структур в двумерных изображениях;
анализ регулярных закономерностей в одномерных рядах данных.

Прежде чем перейти к основной части, разберем ряд определений и основных понятий, которые будут использоваться в дальнейшем.

Определения

Согласно Мандельброту фракталом называется самоподобное множество, имеющее размерность Хаусдорфа-Безиковича строго большую его топологической размерности.

На самом деле, это определение не может претендовать на полноту. Во-первых, математически можно построить фрактальное множество, которое не будет обладать свойством самоподобия. Во-вторых, можно построить фрактал, который будет иметь размерность Хаусдорфа-Безиковича не большую, а меньшую топологической размерности предфракталов на каждой из итераций построения.

В целом следует признать, что удовлетворительного определения фрактала не существует, хотя большинству исследователей интуитивно понятно, о чем идет речь.

В данной работе нас будет интересовать исключительно свойство самоподобия фракталов. Поэтому мы возьмем за основу частное определение, которое сформулировал Мандельброт в работе [1]:

"Фрактал - это структура, состоящая из частей, которые в каком-то смысле подобны целому".

Размерность Хаусдорфа-Безиковича

Пусть имеется компактное множество E в метрическом пространстве R. Рассмотрим покрытие этого множества произвольными односвязными всюду плотными в R подмножествами S_i. Пусть также имеется величина:

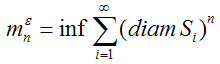$m_n^\varepsilon = \inf \sum\limits_{i = 1}^\infty {(diam\,S_i )^n}$ ,

где нижняя грань берется по всем таким счетным покрытиям {S_i}, для которых diam S_i < 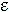$\epsilon$ .

Тогда точная верхняя граница этой величины

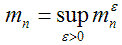$m_n = \mathop {\sup }\limits_{\varepsilon > 0} m_n^\varepsilo}$ ,

называется n-мерной мерой множества E. Максимальное значение n, при которой мера m_n > 0, называется размерностью Хаусдорфа-Безиковича данного множества E.

При меньших значениях n n-мерная мера бесконечна; при больших – равна нулю (рис. 1). Следует обратить внимание на то, что конечное ненулевое значение в точке n = n мера имеет только в том случае, если множество компактно. В противном случае, например, для бесконечной прямой, мера не имеет конечного значения в точке n = n, и при n > n сразу же принимает нулевое значение.

Рис. 1. Поведение меры в зависимости от размерности

Проиллюстрируем практическое применение этого определения на трех примерах.

Пример 1. Размерность кривой линии

Для покрытия произвольной кривой линии шарами диаметра d нам необходимо не более L/d таких шаров. Мера линии, являющаяся ее длиной, приближается к конечному значению по мере уменьшения диаметра шаров покрытия (рис. 3).

Рис. 3. Определение фрактальной размерности линии

По мере уменьшения диаметра каждого шара (d) и увеличения их количества (N), мера m_d¹ = Nd стремится к конечному значению m₁, равному длине кривой (в данном случае - 130 мм) (рис. 4).

Рис. 4. По мере увеличения количества шаров покрытия, частные значения меры (Nd) стремятся к конечному значению

Тогда, исходя из (1) и (2), мы получаем, что размерность Хаусдорфа для кривой линии равна 1

Пример 1. Размерность плоского квадрата

Рассмотрим покрытие единичного квадрата шарами диаметра d в метрическом пространстве R². При диаметре шара, равном диагонали квадрата, для его покрытия достаточно одного шара. При уменьшении диаметра шара вдвое – количество шаров покрытия увеличивается до четырех. При d = ¹/₄ от диаметра исходного шара, нам нужно уже 16 шаров для покрытия квадрата (рис. 5).

Рис. 5. Определение фрактальной размерности единичного квадрата

Несмотря на то, что при таком покрытии сумма степеней диаметров не является точной нижней границей, мы можем показать, что именно при n = 2 мера m_n имеет конечное ненулевое значение.

Количество шаров, необходимых для покрытия единичного квадрата, определяется выражением N = 1/d².

Тогда m_dⁿ = Nd ⁿ = d ⁿ/d ². Очевидно, что при n < 2 соотношение d ⁿ/d ² стремится с уменьшением d – к бесконечности, а при n > 2 – к нулю. К конечному значению мера m_dⁿ стремится лишь при n = 2. Это и есть размерность Хаусдорфа для плоского квадрата.

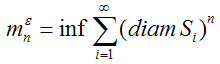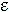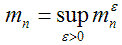К списку разделов

Следующий раздел: Системы итерируемых функций